1.3 Assign values (or ‘weights’) to all dyadic relationships.
Here, I use 4 different scenarios:
1. Scenario (S1): Within-group relationships (wgr) are relatively strong in comparison to between-group relationships (bgr). Relationships of individuals between ‘close groups’ (bcgr) are intermediate.
2. Scenario (S2): Similar to S1, but differences between wgr, bcgr, and bgr are smaller.
3. Scenario (S3): Wgr are relatively strong in comparison to bgr. This scenario is identical to S1 except that there are no close groups.
4. Scenario (S4): Differences between wgr and bgr are smaller than in S3. This scenario is identical to S2 except that there are no close groups.
Thus, bgr are the same in all four scenarios, only bcgr and wgr are varied. Furthermore, wgr are the same for S1 and S3, and for S2 and S4 (see plot below).
To create the social networks, I sample values from beta distributions simulating an Association Index. Such an index is commonly used in animal behavioural research to assess relationships between individuals (see, e.g., the great book by Whitehead, 2008), and they range from 0 to 1. For example, individuals that never associate with each other would have an association index of 0, and two individuals that are always associated with each other have an index of 1.
bgr <- c(1, 8)
bcgr_1 <- c(3, 8)
wgr_1 <- wgr_3 <- c(8, 8)
bcgr_2 <- c(1.5, 8)
wgr_2 <- wgr_4 <- c(4, 8)
plot_beta <- function(x, alpha_beta, main = "", xlab = "", ylab = "", ...){
alpha = alpha_beta[1]
beta = alpha_beta[2]
plot(x, dbeta(x, alpha, beta), type = "l",
yaxt = "n", xlab = "", ylab = "", bty = "n", ...)
title(ylab = ylab, line = 0)
title(xlab = xlab, line = 2)
title(main = main, line = 1)
axis(side = 2, label = F, lwd.ticks = F)
}
{
par(mfrow = c(4,3), mar = c(3, 2, 2, 1))
x <- seq(0, 1, length.out = 40)
plot_beta(x, bgr, main = "Between-group - S1",
ylab = "Prob. density function")
plot_beta(x, bcgr_1, main = "Between close-groups - S1")
plot_beta(x, wgr_1, main = "Within-group S1")
plot_beta(x, bgr, main = "Between-group - S2",
ylab = "Prob. density function")
plot_beta(x, bcgr_2, main = "Between close-groups - S2",
xlab = "Association Index")
plot_beta(x, wgr_2, main = "Within-group - S2")
plot_beta(x, bgr, main = "Between-group - S3",
ylab = "Prob. density function")
plot.new()
plot_beta(x, wgr_3, main = "Within-group - S3")
plot_beta(x, bgr, main = "Between-group - S4",
ylab = "Prob. density function",
xlab = "Association Index")
plot.new()
plot_beta(x, wgr_4, main = "Within-group - S4",
xlab = "Association Index")
}
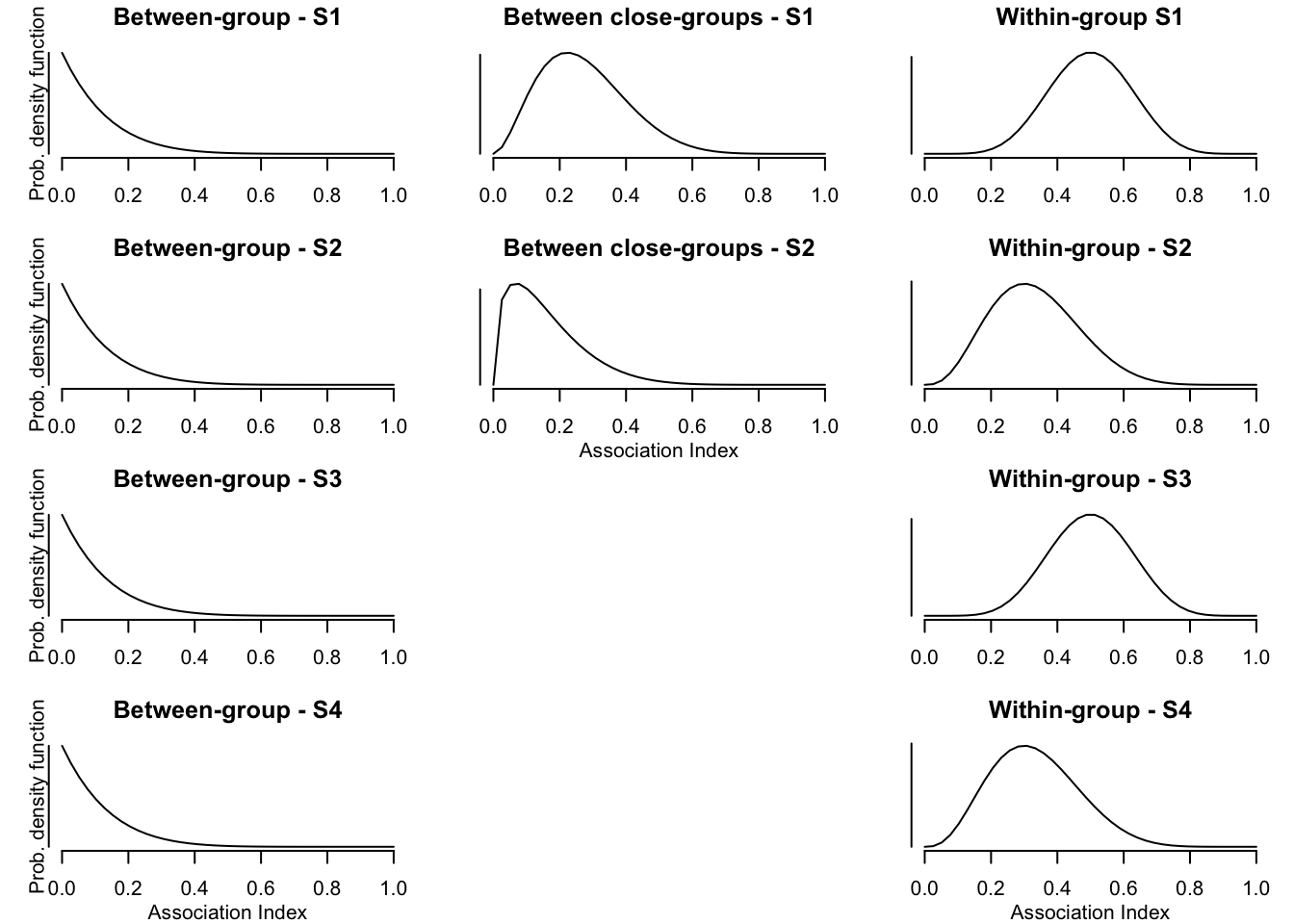
These distributions can be used to get values for the strength of relationships. To do so, I first define a function to sample dyadic values from the different distributions depending on group membership of both individuals. Then, I use this function to get values for all dyads and for all scenarios. For S1 and S2, group A and B are defined as the close groups.
get_weights <- function(network_df, wgr, bgr, bcgr = NA, close_groups = NA){
weights = rep(NA_real_, time = nrow(network_df))
for(i in seq_along(weights)){
ind_A_group <- network_df[i, "Ind_A_Group"]
ind_B_group <- network_df[i, "Ind_B_Group"]
if(ind_A_group == ind_B_group){
weights[i] <- rbeta(n = 1, shape1 = wgr[1], shape2 = wgr[2])
}
if(ind_A_group != ind_B_group){
weights[i] <- rbeta(n = 1, shape1 = bgr[1], shape2 = bgr[2])
}
if(all(!is.na(bcgr)) & all(!is.na(close_groups)) &
ind_A_group != ind_B_group &
ind_A_group %in% close_groups &
ind_B_group %in% close_groups){
weights[i] <- rbeta(n = 1, shape1 = bcgr[1], shape2 = bcgr[2])
}
}
return(weights)
}
set.seed(1209)
network_df$S1 <- get_weights(network_df, wgr = wgr_1, bgr = bgr, bcgr = bcgr_1,
close_groups = c("group_a", "group_b"))
network_df$S2 <- get_weights(network_df, wgr = wgr_2, bgr = bgr, bcgr = bcgr_2,
close_groups = c("group_a", "group_b"))
network_df$S3 <- get_weights(network_df, wgr = wgr_3, bgr = bgr)
network_df$S4 <- get_weights(network_df, wgr = wgr_4, bgr = bgr)
As the last step for part 1 of this post, I will illustrate the created networks using the ggraph package (look here for an introduction to this package by the author)
set.seed(1209)
clustered_network_plot <- network_df %>%
pivot_longer(cols = matches("S\\d"),
names_to = "Scenario",
values_to = "weight") %>%
select(from = Ind_A, to = Ind_B, weight, Scenario) %>%
filter(weight >= 0.3) %>%
as_tbl_graph() %>%
activate(nodes) %>%
left_join(distinct(individual_df, name = Ind, group = Group),
by = "name") %>%
ggraph(., layout = "fr") +
geom_edge_arc(aes(width = weight),
alpha = 0.4, strength = 0.1) +
scale_edge_width(name = "Association Index",
range = c(0.2, 1)) +
geom_node_point(aes(fill = group, shape = group),
size = 2) +
scale_fill_brewer(type = "qual", palette = 2) +
scale_shape_manual(values = c(21, 22, 23, 24)) +
facet_edges(~Scenario) +
theme_graph()
clustered_network_plot
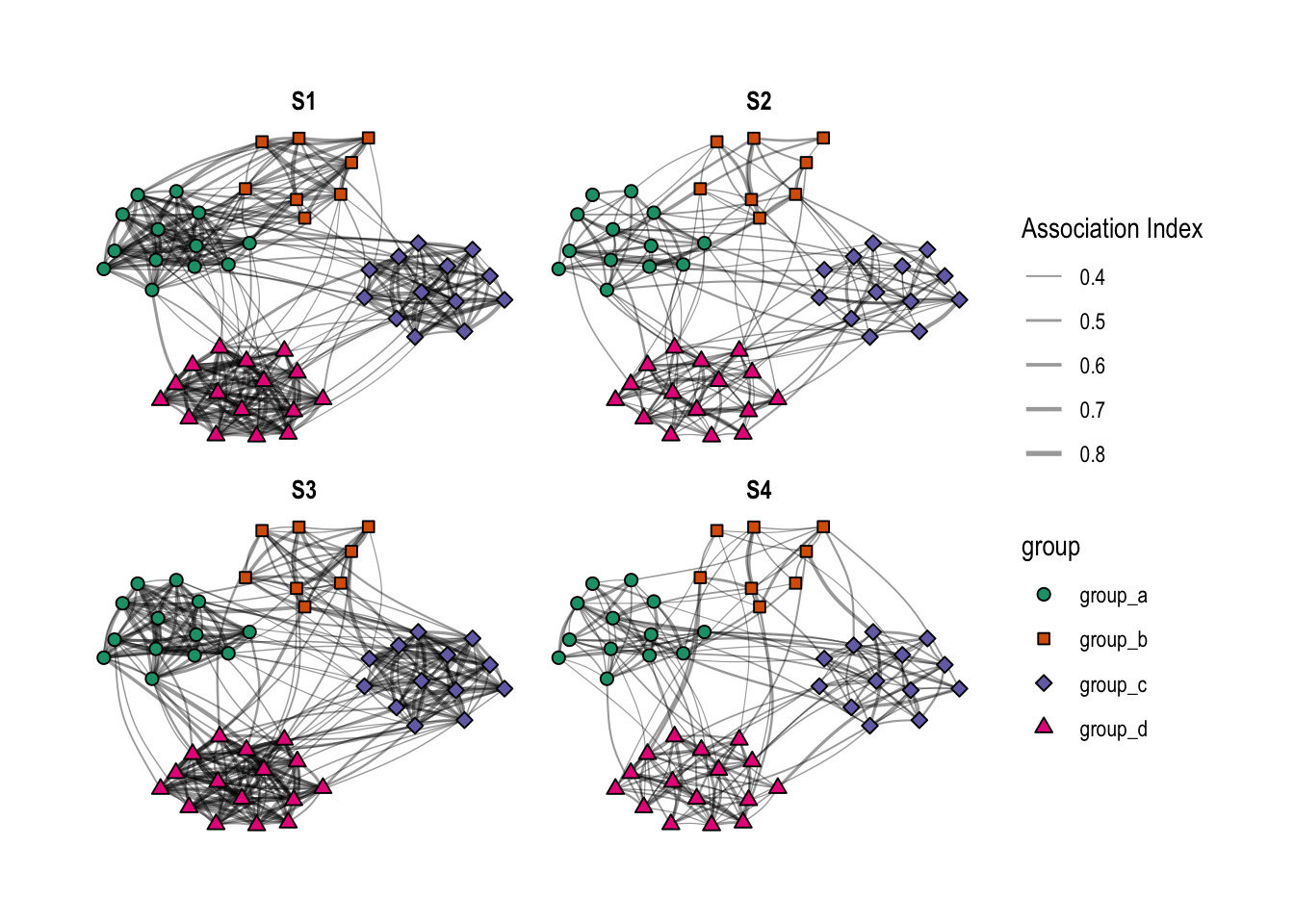 As modeled above, S1 and S3 are very similar, except that group A and B are closer to each other in S1. S2 and S4 have both weaker within-group relationships compared to their counterparts S1 and S3, respectively. Thus, I have four different networks with different degrees of clustering, and in two of these networks, two of the four groups are closer to each other than to the other groups.
As modeled above, S1 and S3 are very similar, except that group A and B are closer to each other in S1. S2 and S4 have both weaker within-group relationships compared to their counterparts S1 and S3, respectively. Thus, I have four different networks with different degrees of clustering, and in two of these networks, two of the four groups are closer to each other than to the other groups.
In the next post, I will use different algorithms from the igraph package to check how well these clusters can be detected.
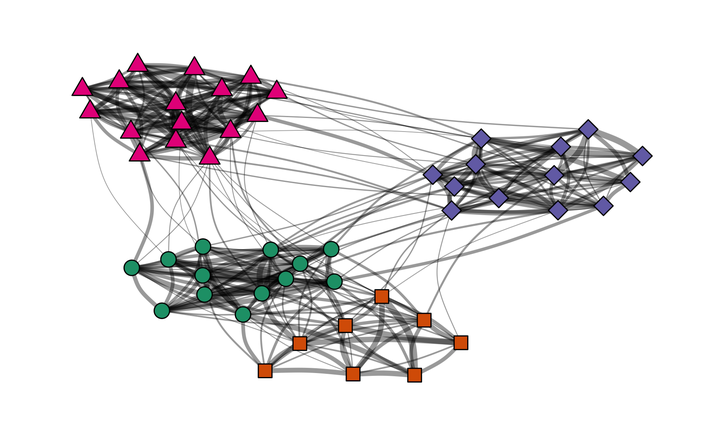

 As modeled above, S1 and S3 are very similar, except that group A and B are closer to each other in S1. S2 and S4 have both weaker within-group relationships compared to their counterparts S1 and S3, respectively. Thus, I have four different networks with different degrees of clustering, and in two of these networks, two of the four groups are closer to each other than to the other groups.
As modeled above, S1 and S3 are very similar, except that group A and B are closer to each other in S1. S2 and S4 have both weaker within-group relationships compared to their counterparts S1 and S3, respectively. Thus, I have four different networks with different degrees of clustering, and in two of these networks, two of the four groups are closer to each other than to the other groups.